Úvod
V tomto příspěvku si ukážeme konkrétní práci v softwaru Statistica, a to sice při detekci vlivu jednotlivých faktorů na chování laboratorních krys v bludišti.
Data
Máme tři kmeny krys, jejichž obecná schopnost úspěšně se pohybovat v bludišti by se dala popsat jako dobrá, nestálá, nebo špatná. Čtyři krysy z každého kmenu byly vychovávány ve stimulujícím prostředí, čtyři v prostředí omezeném. Cílem je určit, zda kmen, prostředí nebo obojí má vliv na počet chyb, které krysa v bludišti udělá. Data k tomuto příkladu jsou v anglické podobě tohoto výukového příkladu v Soubor / Otevřít příklady / Datasets / Rats.sta.
Analýza – postup
Neváhejte a pojďte si tento příklad krok za krokem „naklikat“ s námi.
Po načtení dat v softwaru Statistica volíme: Statistiky / ANOVA / dialog Obecná ANOVA/MANOVA – Vícefaktorová ANOVA (jako Typ analýzy), v poli Metoda specifikace ponecháme Rychlé nastavení. Klikneme na OK. Zobrazí se dialog ANOVA/MANOVA Vícefaktorová ANOVA. Klikneme na tlačítko Proměnné a zvolíme Chyby jako závislou proměnnou a Kmen a Prostředí jako kategoriální prediktory. Klikneme dvakrát na OK a dostaneme se tak do dialogu ANOVA Výsledky. Tento dialog poskytuje spoustu možností pro volbu nejrůznějších výsledků. Jsou uspořádány na osmi záložkách.
Pokud je vám tento počet záložek málo, tak je možné přepnout do ještě obsáhlejšího výsledkového dialogu stiskem tlačítka Více výsledků.
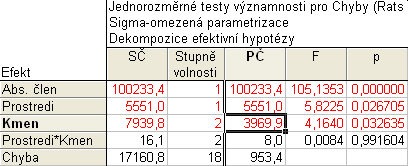
Zpět do původního výsledkového dialogu se vrátíte stiskem tlačítka Méně. Nyní kliknutím na tlačítko Všechny efekty/grafy na záložce Základ zobrazíme dialog Tabulka všech efektů. Oba efekty (Prostředí i Kmen) jsou označeny jako významné (jsou označeny hvězdičkou *), ale efekt interakce (Prostředí*Kmen) významný není.
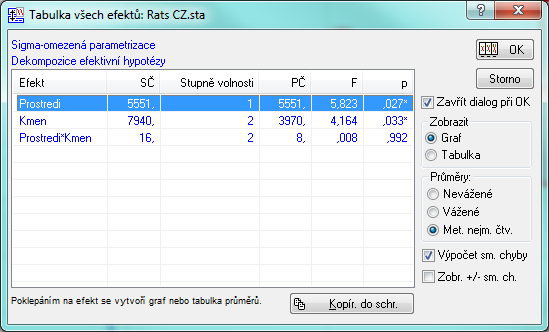
Poznámka: V praxi bychom model po těchto zjištěních pravděpodobně nadefinovali znova bez interakcí, tedy v menu dialog Obecná ANOVA/MANOVA nezvolíme Vícefaktorová ANOVA, ale ANOVA hlavních efektů.
Nicméně protože je vliv interakcí na výsledek nepatrný, a navíc si budeme moci ukázat, jak nevýznamné interakce poznat z grafu, budeme proto pokračovat v modelu s interakcemi.
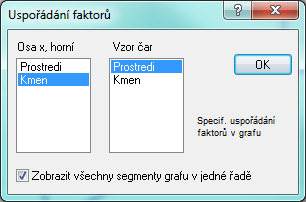
U analýzy rozptylu jsou marginální průměry jednou z hlavních charakteristik, které nám o souboru něco řeknou. Je možné je jednoduše vypočítat a zobrazit, například po vybrání (kliknutím) efektu interakce (Prostředí*Kmen) v tabulce výše (Tabulka všech efektů) a klikneme na OK. Zobrazí se dialog Uspořádání faktorů, v němž určíme, jak bude vypadat vytvořený graf. Pro účely tohoto příkladu nastavíme Kmen v seznamu Osa x, horní a Prostředí v seznamu Vzor čáry:
Kliknutím na OK vytvoříme příslušný graf. Jasně vidíme, že krysy vychované v omezeném prostředí, dělaly více chyb než krysy vychované ve stimulujícím prostředí nezávisle na kmeni. Současně krysy se špatnou schopností orientovat se v bludišti dělaly nejvíc chyb, nejméně jich dělaly chytré krysy.
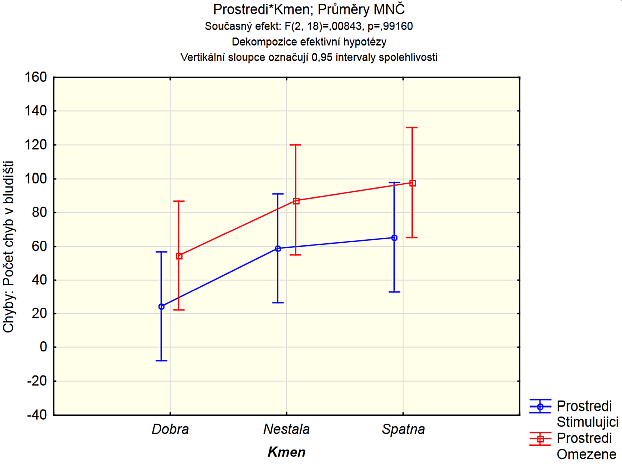
Z grafu je také vidět nevýznamnost interakcí, neboť obě křivky jsou rovnoběžné.
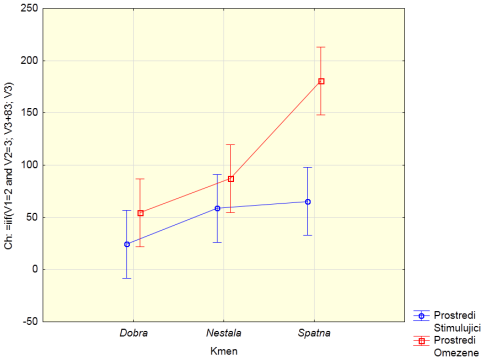
Poznámka: Uveďme pro ilustraci i případy, jak by měl vypadat graf, který by významnost interakcí naopak prozrazoval. Tím by mohl být graf, kde by se jednotlivé spojnice průměrů faktorů křížily, nebo by se střední hodnota závisle proměnné v určité kombinaci faktorů významně odlišovala. V těchto případech by pravděpodobně šlo o statisticky významnou interakci. Druhý popisovaný případ ilustruje graf.
Výsledky ANOVA lze zobrazit také ve formě tabulky kliknutím na tlačítko Všechny efekty na záložce Základ. Významné efekty jsou zvýrazněny červeně.
Post-hoc testy
Jak již bylo řečeno, v této analýze se projevil významný efekt faktorů Prostředí a Kmen. Zdůrazněme ovšem, že test významnosti nám neříká nic o tom, která (nebo které) ze skupin krys se od ostatních v počtu chyb významně liší. Abychom to zjistili, můžeme provést Post-hoc testy. Klikneme na tlačítko Více výsledků a následně na záložku Post-hoc:
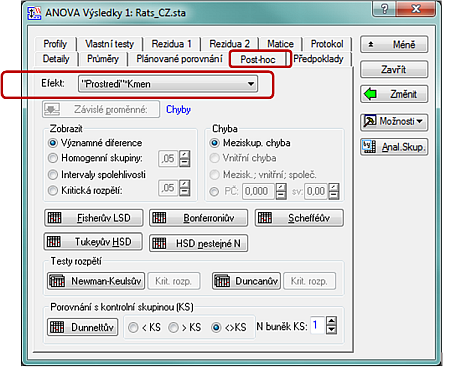
V poli Efekt zvolíme Kmen, abychom mohli provést porovnání marginálních průměrů pro tento efekt. Kliknutím na tlačítko Schefféův se v tabulce zobrazí výsledky Schefféova testu:

Tato tabulka zobrazuje statistickou významnost rozdílů průměrů pro všechny páry skupin krys. Jak je vidět, pouze rozdíl mezi 1. a 3. skupinou, tj. mezi hloupými a chytrými krysami, je statisticky významný na hladině významnosti 0,05. Lze tedy utvořit závěr, že pouze hloupé krysy dělaly významně více chyb než krysy chytré, zatímco průměrné krysy se od zbývajících dvou skupin nijak významně neliší.
Předpoklady
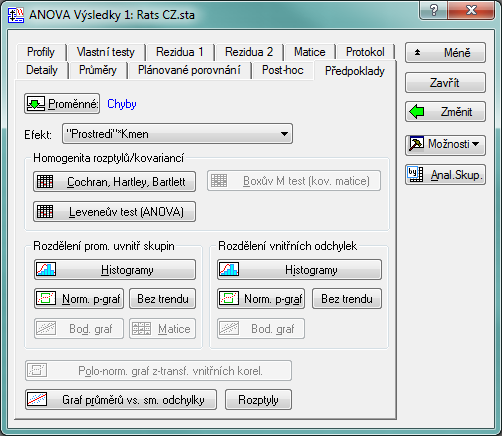
Výsledky samotné analýzy rozptylu máme. Ale jak naznačuje obrázek elektronické sestřičky našich zkoumaných krys, čeká nás ještě další klikání. Samozřejmě je třeba otestovat předpoklady, za kterých lze metodu ANOVA uplatňovat. Přepneme se proto na záložku Předpoklady:
Normalita
Prvním předpokladem analýzy rozptylu, který si ověříme, je normalita sledovaných vzorků. Musíme tedy ověřit předpoklad, že rozdělení závislé proměnné v jednotlivých skupinách je normální. Pro posouzení typu rozdělení závislé proměnné lze využít například normální pravděpodobnostní grafy, které jsou dostupné přímo na kartě Předpoklady. Nebo přes menu Grafy / 2D Grafy / Normální pravděpodobnostní grafy… Přes záložku Grafy lze však zaškrtnout jako doplněk výstupu Shapiro–Wilkův test, pomocí kterého lze otestovat nulovou hypotézu o normalitě konkrétního vzorku a tím podpořit vizuální odhad průběhu.
Poznámka: Normální pravděpodobnostní grafy slouží jako vizuální pomůcka při testování předpokladu normality – čím blíže jsou body v grafu okolo vykreslené přímky, tím blíže jsme normálnímu rozdělení. Pozor bychom si měli dávat především na nějaké systematické odchýlení od přímky, například esovitý průběh.
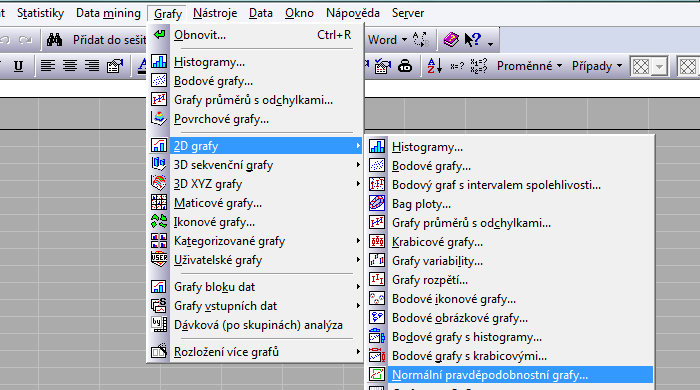
V případě, že by se jednalo o posouzení normality z hlediska úrovně jednoho faktoru, potom je jednoduché si přes záložku Analýza po skupinách skupinový vzorek „rozgrupovat“:
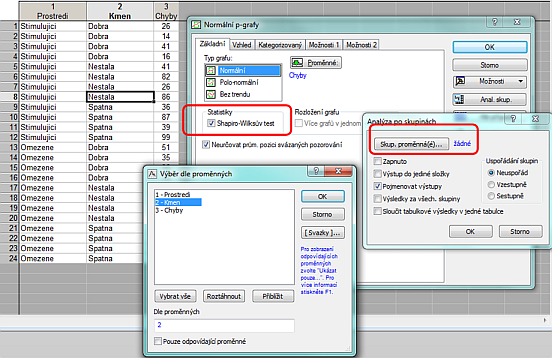
V případě více faktorů a interakcí již není úplně jednoduché postihnout všechny možnosti, resp. v jednotlivých skupinách je následně velmi malé množství dat, bude proto lepší předpoklad normality otestovat po samotném odhadu parametrů modelu přímo na jeho reziduích. Přepneme na záložku Rezidua, ve které máme bohaté možnosti, jak se na tento vektor dívat. Buď se podíváme na normalitu reziduí přímo kliknutím na P-graf reziduí nebo to můžeme udělat ve dvou krocích, nejdříve si vygenerujeme rezidua do pracovního sešitu Statistica, to uděláme klepnutím na tlačítko Předpovědi a rezidua. V sešitu Statistica poté označíme tabulku reziduí jako aktivní vstup:
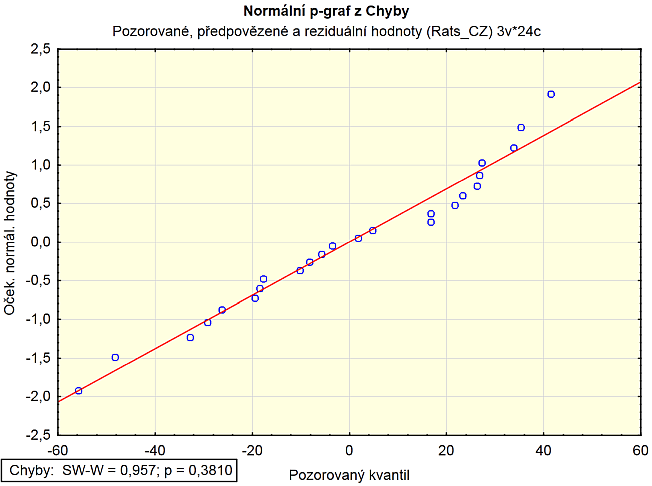
A zobrazíme si opět Normální pravděpodobnostní graf (přes menu Grafy) a výsledky Shapiro-Wilkova testu, ze kterého si potvrdíme (p = 0,3810) vizuální odhad průběhu dat, tedy že nezamítáme nulovou hypotézu o reziduích.
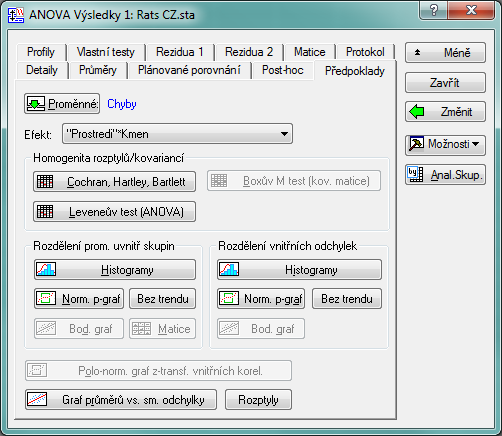
Dále je možné využít celé řady grafů, které jsou na kartě Rezidua přímo v analýze ANOVA.
Homogenita rozptylů
Dalším z předpokladů je homogenita rozptylů mezi skupinami. Statistica poskytuje několik testů tohoto předpokladu ve skupině Homogenita rozptylů/kovariancí na záložce Předpoklady. Vzhledem k normalitě dat použijeme pro účely tohoto příkladu Leveneův test (ANOVA).
Níže uvedená tabulka s výsledky tohoto testu nevykazuje žádné údaje indikující, že by rozptyl v jednotlivých skupinách byl statisticky významně odlišný (tj. podmínka homogenity rozptylů je splněna).

Tím jsme ověřili předpoklady pro použití metod analýzy rozptylu na data s krysami. Více informací o možnostech v dialogu ANOVA výsledky se můžete dozvědět v odborném kurzu Analýza rozptylu.
Závěr
Jak se zdá z výsledků analýzy, můžeme s velkou pravděpodobností říci, že faktory genetických dispozic i prostředí výchovy mají významný efekt na schopnost krys pohybovat se v bludišti.